ABCdario de las Matemáticas
ABC Science
The ‘magic square of Foz’, the ‘fozudokus’ and mathematics from Lugo
- A reader of the ABCdario de las Matemáticas proposes a challenge: a variant of the sudoku Galician style.

(updated 05/31/2021)
Many of the articles published in newspapers and magazines on recreational mathematics (and on other topics) sometimes mention contributions from readers, who propose suggestions, refute arguments, express doubts, resolve questions raised, or offer information related to the topic being discussed. In this ABCdario of Mathematics some appear in the comments, and others reach the authors through e-mails. All are read, and some answered, although we wish we had more time to devote more attention to them. And it is really enriching to meet and exchange ideas and opinions most of the time.
At the end of December of last year, I received one of these emails asking me questions about a game invented by the sender. Today I am going to describe this pastime because once seen in some detail it seems to me of interest, especially because of the final message that I want to convey to you, and because I believe that its author deserves to be known about his invention, and our applause. Before I introduce you a couple of concepts on which it is based, which most of you surely know, but which it is worth remembering very schematically.
Magic Squares
In previous reviews we have already talked about them see one example and another A magic square is an arrangement of numbers in a square (they can be consecutive, only even, only odd, only prime, repeated or not, etc., there is no restriction, although the ‘classics’ are consecutive from 1 onwards) of so that all the rows, all the columns, and the two diagonals of the square add up to the same value (not only are there additives, but the operation can also be multiplication, in this case being called multiplicative magic squares). The order of the magic square is called the number of squares that each row (or column) has.
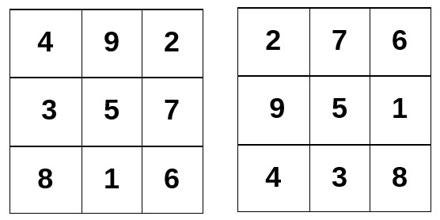
Obviously, order one is a triviality, order two (with the numbers from 1 to 4) that arrangement is not possible, and the thing begins to be interesting with order three, trying to arrange the numbers from 1 to 9 complying with these rules . There is only one arrangement that verifies it (no twists or symmetries are counted; in the image you can see it in two versions, but it is the same square: in the second, the rows of the first have simply been placed as columns, and from bottom to top), and is known from 2200 a. C., the famous Chinese Lo-Shu.
With order four, that is, arranging the numbers from 1 to 16, there are 880 different configurations. It was the French amateur mathematician Bernard Frénicle de Bessy who exhibited this figure at the Academy of Arts in Paris in 1676, and Philippe de La Hire who listed all of them in 1693. It has been shown that there are 275305224 magic squares of order 5, but for larger orders knowing their exact number is an unsolved problem (only rough estimates are available for now).
One of those magic squares, famous for appearing in Albrecht Dürer’s Melancholy (1514) engraving is the one shown in the following image.
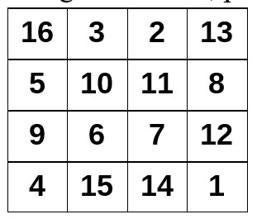
In addition to indicating the date of completion of the engraving in the lower central boxes, it is unique because there are 24 different configurations that add up to 34, the magic constant for squares of order four. I suppose you know why it is precisely 34: the numbers from 1 to 16 add up to 136, and since they have to be distributed among four rows, each one must add 136/4 = 34. There is no mystery, no matter how much we want to remove it from the adjective ‘magic ‘. The 24 different configurations are as follows:
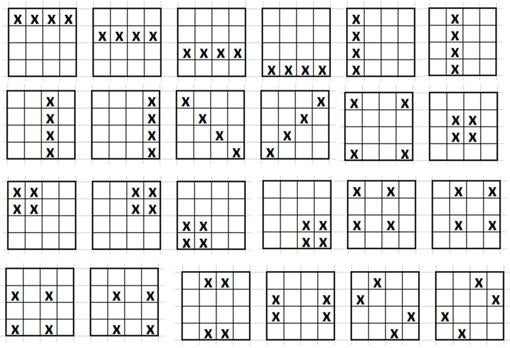
There is some configuration that adds 34, as is the movement of the chess knight 3 – 8 – 14 – 9 and 2 – 12 – 15 – 5. But we are going to focus only on the 24 reflected in the previous image. If we swap the second and third columns of the magic square, we get this other configuration:
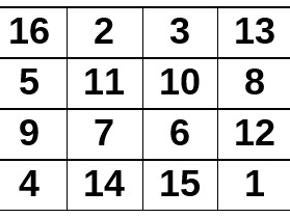
It is another of the 880 possible magic squares of order four, which still fulfills that the 24 configurations of four figures described above add up to 34. We are left with this magic square and those configurations.
From a mathematical point of view, magic squares have always been considered an entertainment, a curiosity without much application, except as the basis of some magic tricks.
Latin Squares
A Latin square (so named by Leonhard Euler around 1779 simply because he used Latin letters in his composition) is a square arrangement of symbols (they can be letters, numbers, colours, drawings, anything) in which each symbol is never repeated in the same row or column (mathematically each row or column is a different permutation of the elements of the others). There is no arithmetic operation (unlike magic squares), the objects are simply arranged as described. Sudokus are an example of a Latin square that uses the digits 1 to 9.
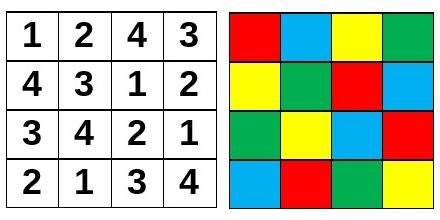
In the image appears a Latin square of order four with numbers and the same with colors. Of order four there are 576 different Latin squares. If we add the condition that there is also no repetition in the two diagonals (diagonal Latin square), then there are only 2 different ones (the one shown before is one of them, could the reader find the other?).
Unlike magic squares, Latin square theory constitutes an active field of mathematical research, as it is key in solving certain types of problems, and has an intrinsic group structure. There are many open questions (raised and unresolved) that involve these types of squares
THE FOZUDOKUS
Antonio Pomares Olivares is a retired British Post Office employee who has lived in London for over fifty years. At the age of thirteen, he stopped studying to go to work, with which his mathematical knowledge is basic, although he declares himself fond of recreational mathematics, in particular the magic squares that his father showed him as a child.

In one of his summers in Foz (Lugo), specifically in 2014, playing with coloured magnets, he realized the possibility of placing them in four rows without repeating any (the structure of a Latin square that we have discussed) and he joins the magic square of order four described above, forming the following configuration (in the image, the composition that he has captured on the facade of his Galician house).
In addition, he devises an algorithm to generate the square from the natural order of the figures with them hidden and staged it as a magic trick (not exactly because magicians do not reveal their methods and Antonio does, he has no problem explaining them). In this home video (from minute 1:15), he does it.
There is no doubt that this procedure is his creation, because in reality the construction of this square is much simpler (although less spectacular to pass it off as
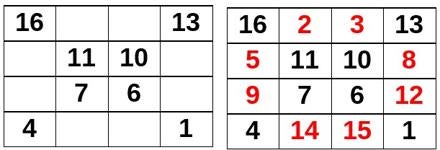
‘something magical’, of course): the well-known X method of composing even-order magic squares is much simpler. It is about placing, either starting from the top, or from the bottom, it does not matter (I show it from below so that it remains the same as his), the natural numbers in their usual order only on the diagonals of the square, as seen in the picture.
Then we make a second pass from above, placing, also in their natural order, the missing numbers (in red). Thus, with only two steps, we build the square, much simpler and faster than Antonio’s procedure, which does it in three steps and with quite convoluted changes. Between the friends he tells about it and himself, they decide to ‘baptize’ the square with the name of the town they are in, and call it ‘Magic Square of Foz’.
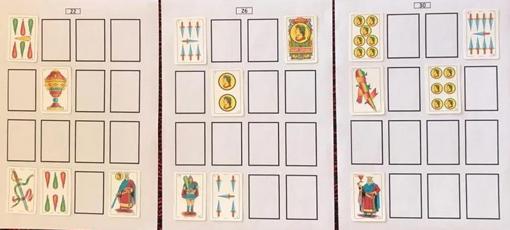
Well, so far, nothing that was not known. The second part is the interesting one, and in my opinion, novel (at least I have not located it anywhere else; it has been called Fozudoku). Transfer the idea to a deck of cards, in which now the numbers are the values of the card, and the colours are the suits (cups, swords, golds and clubs). Normally we use the Spanish deck of 40 cards, but he adds the necessary ones to play poker, that is, he adds the eights and nines, so we have 48 cards, from 1 to 12 of each suit.
With them he can build three magic squares of order four. Beware: magic card squares, not numerical ones. That is, in each magic square, the rows, columns and diagonals are going to be different cards, understanding by different, of different numerical value and different suit, because necessarily with four aces, for example, for only three squares, obviously in some repeats the numeric value. Furthermore, it will require, as with Dürer’s magic square and its variant, that there be other combinations with the same sum. Specifically, the same 24 as indicated above. With these conditions, Antonio has devised a five-step algorithm, in which all the cards in the deck can be arranged with those conditions, so that the first square adds 22, the second 26 and the third 30.
After placing all of them face down (without seeing them) by means of this algorithm, five are discovered, and from them, it is a matter of trying to guess which is each covered card. A good pastime (like Sudoku, in which you also must do sums) that attracts the attention of primary school children and older people in the places where it has been explained (schools, associations, among others).
MATHEMATICAL QUESTIONS
Some questions immediately arise. How many such magic squares can be built? Is it mandatory to uncover five to solve them? Could it be with less? Could other triples be constructed in which the sum of the squares is different? Can you find other algorithms that build Fozudokus of this type? The repeating numerical values in which you have built (not the letters, we clarify again) are (1, 2, 3, 4) for the first, (5, 6, 7, 8) for the second and (9 , 10, 11, 12) for the third. Could they be composed with other different repetitions? Antonio Pomares has also thought about these and other questions. At the moment he is focused on discovering how many there are of the kind he has devised. So far he has composed 365 different possibilities, but he does not know if they are all possible or there may be more. Let us remember that his method of work, given his mathematical knowledge, is that of trial and error. Surely among the readers they can give you some indication or advice to solve your question.
Antonio has also thought of different variants. For example, on how to use this as a game between two, not just as a solitaire: the five cards of each of the three squares are proposed (there are 33 left to place), 10 cards are dealt to each player, leaving a deck with 13 cards which are placed face down on the table. Alternatively, each player places a card on the squares according to the rules, and when he cannot (or does not know) place any of the remaining ones, he draws from the deck until he finds one that he can place. The winner is obviously the player who finishes laying down all his cards first. However, he has been refining the rules based on the experiences of people who have played the game that have come to him, since, with a little practice from both players, those conditions always lead to a tie.
He has also adapted the idea to the French poker deck, and devised a variant for magic stars and crosses. And he has developed an even more complex case in which the Fozudokus must verify 36 different combinations, instead of the 24 mentioned. He has called it ‘Fozudoku of the wall’, and the solution seems to be unique.
All the information, details, example videos, files with all the possibilities, absolutely everything that has been deduced is shared in several languages at this link.
FINALLY
It is clear that games like this are good exercise for both children and adults, helping to develop and maintain our mental agility. But above all, it has been, and is, a personal challenge for Antonio himself, an incentive with which to occupy and enjoy the hours of the day, also providing something beneficial for everyone. Mathematics (also other disciplines, such as literature, history, painting, music, actually any human activity) allows people to investigate, learn and share knowledge. The difference is that some require more effort or specific skills (reading a lot, writing well, having a good ear, etc.) and paradoxically, despite being considered a complex discipline, mathematics has many levels of depth, and as we see, with little thing, with very simple content, we can enter, with ingenuity and perseverance, in exciting and even relevant matters.
With the Fozudokus, in addition to activities in some educational centers in Foz, Alicante (Antonio’s hometown; for example, in the El Templete de Benalúa Neighbourhood Association), London (including a deaf-mute center), this pastime was used in the ‘Julia Robinson Mathematical Festival’, a virtual cruise through 22 Latin American countries in which different aspects of mathematics were worked on through games, held last April. Thanks to the collaboration of friends, neighbours and other people, this initiative is making its way through the networks, the media, etc. Let the example spread !!
Alfonso Jesús Poblacion Sáez is a professor at the University of Valladolid and a member of the Dissemination Commission of the Royal Spanish Mathematical Society (RSME).
The ABCdario de las Matemáticas is a section that arises from the collaboration with the RSME Dissemination Commission.

El periódico EL PROGRESO (25 abril 2013)
https://www.elprogreso.es/articulo/noticias/matematicas-magia-e-ingles/20130425110000262111.html
Yesterday’s afternoon at the Martínez Otero School in Foz was very special thanks to
the performance of the mathematician, Antonio Pomares Olivares, who gave a
mathematics in English as part of the centre’s language immersion activities.
The activity was designed for students in the third cycle of primary school and ESO and consisted of a series of games based on the mathematical magic squares using the Sudoku technique and the classic Spanish deck.
«It was an interdisciplinary academic activity, because the mathematical mental processes, of logical thinking and calculation and linguistic processes were involved, because the activity was entirely in English,» explained the school’s director, Tono Alonso.
This is not the only different activity that the students were able to enjoy during this week, as since last Thursday the campaign ‘Open a book, open the world’ has been underway at the school, which aims to encourage and motivate children and young people to enjoy reading.
The campaign consists of reading texts every day, until tomorrow, during the first five minutes of class, alluding to the need and benefits that reading has for children and adults.
These are texts by authors as diverse as Miguel Indurain, Rosa Montero and Jorge Luis Borges, who try to transmit a taste for books.
With this type of event, children enjoy different things that stimulate their desire to learn.
.
El periódico La Voz de Galicia (30 junio 2013)
Antonio Pomares Olivares Creator of a Mate-magia show
«With my magic square, children can practice sums better» says Antonio Pomares.
«The Magic Square can help children to add»
He has already taken his show, The Wizard of Foz, to three Foz schools
YOLANDA GARCIA – FOZ / THE VOICE
Mathematics and Magic are twinned giving life to «Mathematics-Magic». And it is put into practice by Antonio Pomares Olivares, a 66 year old retired man, who, through the name of El Mago de Foz, pays homage to the town that welcomes him, as well as those of London and Alicante. His show is based on the magic square, in which the groups of four numbers always add up to 34. This is of Asian origin and Dürer introduced it to Europe through a painting. His unique version, the Magic Square of Foz, has been shown to Foz students and will be shown in San Lourenzo.
How did the idea come about?
I always liked numbers. Now I’m retired and have more time. Last year, I was spinning it with some coloured magnets stuck to the fridge. They can be put in such a way that no colour is repeated. I thought I could do it with the 4 by 4 magic square, improve it. And I moved it to the Spanish deck, which is more complicated. In the magic square I saw a potential to help children practice addition.
Where is the «magic»?
It draws a lot of attention first because everything adds up the same and because 30 of the 48 cards can be guessed. It’s not just a show, but it would be a failure. I want people to keep playing at home alone or with someone else, to activate the mind. This is closer to sudoku.
How do you spread it?
I have a Japanese friend who has designed the website http://cuadrado magicodefoz.com/ and I will also make it known in London and Alicante and to the elderly
.
El periódico EL PROGRESO (9 abril 2020)
articulo-en-el-progreso-9-4-2020Descarga

A 73 year-old from Alicante creates the Fozudoku, which plays with the Spanish deck
Pablo Yáñez | April 09, 2020
Antonio Pomares spends the summer in Foz, where his wife is from. The sudokus and their solutions can be found on his Facebook
The confinement due to the coronavirus pandemic that is taking place in Spain and much of the world, and which will be one month old in a few days, means that boredom may be just around the corner.
To avoid this, Antonio Pomares Olivares, a native of Alicante who spends his summers in Foz, has devised Fozudoku, a sudoku made from a Spanish deck of 48 cards.
This game consists of three squares containing 16 cards each. In each square there are six cards discovered, in total 18 among the three squares, and the remaining 30 must be discovered, as in the game of sudoku, taking into account the 24 groups of four cards that add up to the same thing and without any suit being repeated. The first square on the left adds up to 22, the one in the middle to 26 and the one on the right to 30.
Every day, Antonio Pomares puts a new Fozudoku on his Facebook page and the next day the solution. To date, 19 Fozudoku have been made during this time we are spending at home to avoid contagion and to spread the Covid-19. This Alicante-based company also has a website for this game, which is cuadradomagicodefoz.com.
The idea of this alicantino was to put the name of Spanish Sudoku, but he discarded the idea because he had copyright.
A Japanese friend of his proposed that he name it Foz, where his wife, Dolores Bustamente, was born and where they spend their summers. And so it was.
Today’s children do not have the mental agility that we used to have
Pomares is a great lover of numbers. In the house where he spends his summers in Foz he has, on the facade, a magic square made of coloured tiles.


«Some people like crosswords or wordsearch puzzles and others like Sudoku; I’m more about numbers than letters,» he says from his home in Alicante.
The aim of Pomares is to get children to play this game so that they can use their attention and logic, also using arithmetic: «The children of today do not have the mental agility that we used to have,» says Pomares. «Before we used to play board games, Parcheesi, cards, now they play other things; you now tell a child how much seven and eight add up to and they have to think about it,» he assures.
This Alicante-based man also has a Whatsapp group, which so far has 36 people, where every day he also puts a Fozudoku» and his solutions the next day. Retired, at the age of 73, Antonio worked in the London post office for 35 years, although he also did a number of other jobs. The confinement caught his wife Focega in the British capital and him in Alicante, where they were going to meet at Easter. Something they would not be able to do due to the closure of borders in Spain.
.
Interview on Valadouro Radio / Pepe Peinó
.
Interview by Radio FOZ (6 September 2020)